Physics:Gravity train
A gravity train is a theoretical means of transportation for purposes of commuting between two points on the surface of a sphere, by following a straight tunnel connecting the two points through the interior of the sphere.
In a large body such as a planet, this train could be left to accelerate using just the force of gravity, since during the first half of the trip (from the point of departure until the middle), the downward pull towards the center of gravity would pull it towards the destination. During the second half of the trip, the acceleration would be in the opposite direction relative to the trajectory, but, ignoring the effects of friction, the speed acquired before would overcome this deceleration, and as a result, the train's speed would reach zero at approximately the moment the train reached its destination.[1][better source needed]
Origin of the concept
In the 17th century, British scientist Robert Hooke presented the idea of an object accelerating inside a planet in a letter to Isaac Newton. A gravity train project was seriously presented to the French Academy of Sciences in the 19th century. The same idea was proposed, without calculation, by Lewis Carroll in 1893 in Sylvie and Bruno Concluded. The idea was rediscovered in the 1960s when physicist Paul Cooper published a paper in the American Journal of Physics suggesting that gravity trains be considered for a future transportation project.[2]
Mathematical considerations
Under the assumption of a spherical planet with uniform density, and ignoring relativistic effects as well as friction, a gravity train has the following properties:[3]
- The duration of a trip depends only on the density of the planet and the gravitational constant, but not on the diameter of the planet.
- The maximum speed is reached at the middle point of the trajectory.
For gravity trains between points which are not the antipodes of each other, the following hold:
- The shortest time tunnel through a homogeneous earth is a hypocycloid; in the special case of two antipodal points, the hypocycloid degenerates to a straight line.
- All straight-line gravity trains on a given planet take exactly the same amount of time to complete a journey (that is, no matter where on the surface the two endpoints of its trajectory are located).
On the planet Earth specifically, since a gravity train's movement is the projection of a very Low Earth Orbit satellite's movement onto a line, it has the following parameters:
- The travel time equals 2530.30 seconds (nearly 42.2 minutes, half the period of a Low Earth Orbit satellite), assuming Earth were a perfect sphere of uniform density.
- By taking into account the realistic density distribution inside the Earth, as known from the Preliminary Reference Earth Model, the expected fall-through time is reduced from 42 to 38 minutes.[4]
To put some numbers in perspective, the deepest current bore hole is the Kola Superdeep Borehole with a true depth of 12,262 meters; covering the distance between London and Paris (350 km) via a hypocycloidical path would require the creation of a hole 111,408 metres deep. Not only is such a depth 9 times as great, but it would also necessitate a tunnel that passes through the Earth's mantle.
Mathematical derivation
Using the approximations that the Earth is perfectly spherical and of uniform density [math]\displaystyle{ \rho }[/math], and the fact that within a uniform hollow sphere there is no gravity, the gravitational acceleration [math]\displaystyle{ a }[/math] experienced by a body within the Earth is proportional to the ratio of the distance from the center [math]\displaystyle{ r }[/math] to the Earth's radius [math]\displaystyle{ R }[/math]. This is because underground at distance [math]\displaystyle{ r }[/math] from the center is like being on the surface of a planet of radius [math]\displaystyle{ r }[/math], within a hollow sphere which contributes nothing.
- [math]\displaystyle{ a = \frac{GM}{r^2} = \frac{G\rho V}{r^2} = \frac{G\rho\frac{4}{3}\pi\,r^3}{r^2} = G\rho \frac{4}{3}\pi\,r }[/math]
On the surface, [math]\displaystyle{ r = R }[/math], so the gravitational acceleration is [math]\displaystyle{ g = G\rho \frac{4}{3}\pi\,R }[/math]. Hence, the gravitational acceleration at [math]\displaystyle{ r }[/math] is
- [math]\displaystyle{ a = \frac{r}{R}\,g }[/math]
Diametric path to antipodes
In the case of a straight line through the center of the Earth, the acceleration of the body is equal to that of gravity: it is falling freely straight down. We start falling at the surface, so at time [math]\displaystyle{ t }[/math] (treating acceleration and velocity as positive downwards):
- [math]\displaystyle{ r_t = R - \int_0^t v_t \,dt = R - \int_0^t\int_0^t a_t\,dt\,dt }[/math]
Differentiating twice:
- [math]\displaystyle{ \frac{d^2r}{dt^2} = -a_t = -\frac{r}{R}\,g = -\omega^2\,r }[/math]
where [math]\displaystyle{ \omega = \sqrt\frac{g}{R} }[/math]. This class of problems, where there is a restoring force proportional to the displacement away from zero, has general solutions of the form [math]\displaystyle{ r = k \cos(\omega t + \varphi) }[/math], and describes simple harmonic motion such as in a spring or pendulum.
In this case [math]\displaystyle{ r_t = R \cos \sqrt\frac{g}{R}\,t }[/math] so that [math]\displaystyle{ r_0 = R }[/math], we begin at the surface at time zero, and oscillate back and forth forever.
The travel time to the antipodes is half of one cycle of this oscillator, that is the time for the argument to [math]\displaystyle{ \cos \sqrt\frac{g}{R}\,t }[/math] to sweep out [math]\displaystyle{ {\pi} }[/math] radians. Using simple approximations of [math]\displaystyle{ g = 10\text{ m}/\text{s}^2, R = 6500\text{ km} }[/math] that time is
- [math]\displaystyle{ T = \frac \pi \omega = \frac \pi {\sqrt\frac{g}{R}} \approx \frac{3.1415926}{\sqrt\frac{10}{6500000}} \approx 2532 \text{ s} }[/math]
Straight path between two arbitrary points
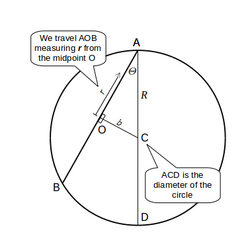
For the more general case of the straight line path between any two points on the surface of a sphere we calculate the acceleration of the body as it moves frictionlessly along its straight path.
The body travels along AOB, O being the midpoint of the path, and the closest point to the center of the Earth on this path. At distance [math]\displaystyle{ r }[/math] along this path, the force of gravity depends on distance [math]\displaystyle{ x }[/math] to the center of the Earth as above. Using the shorthand [math]\displaystyle{ b = R \sin \theta }[/math] for length OC:
- [math]\displaystyle{ g_r = \frac{x}{R}\,g = \frac{\sqrt{r^2+b^2}}{R}\,g }[/math]
The resulting acceleration on the body, because is it on a frictionless inclined surface, is [math]\displaystyle{ g_r \cos \varphi }[/math]:
- [math]\displaystyle{ a_r = g_r \cos \varphi = \frac{\sqrt{r^2+b^2}}{R}\,g \cos \varphi }[/math]
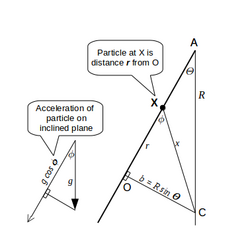
But [math]\displaystyle{ \cos \varphi }[/math] is [math]\displaystyle{ r/x = \frac{r}{\sqrt{r^2+b^2}} }[/math], so substituting:
- [math]\displaystyle{ a_r = \frac{\sqrt{r^2+b^2}}{R}\,g\,\frac{r}{\sqrt{r^2+b^2}} = \frac{r}{R} \, g }[/math]
which is exactly the same for this new [math]\displaystyle{ r }[/math], distance along AOB away from O, as for the [math]\displaystyle{ r }[/math] in the diametric case along ACD. So the remaining analysis is the same, accommodating the initial condition that the maximal [math]\displaystyle{ r }[/math] is [math]\displaystyle{ R \cos \theta = AO }[/math] the complete equation of motion is
- [math]\displaystyle{ r_t = R \cos \theta \cos \sqrt\frac{g}{R}\,t }[/math]
The time constant [math]\displaystyle{ \omega = \sqrt\frac{g}{R} }[/math] is the same as in the diametric case so the journey time is still 42 minutes; it's just that all the distances and speeds are scaled by the constant [math]\displaystyle{ \cos \theta }[/math].
Dependence on radius of planet
The time constant [math]\displaystyle{ \omega }[/math] depends only on [math]\displaystyle{ \frac{g}{R} }[/math] so if we expand that we get
- [math]\displaystyle{ \frac{g}{R} = \frac{GM/R^2}{R} = \frac{GM}{R^3} = \frac{G\rho\,V}{R^3} = \frac{G\rho\,\frac{4}{3}\pi\,R^3}{R^3} = G\rho\,\frac{4}{3}\pi }[/math]
which depends only on the gravitational constant and [math]\displaystyle{ \rho }[/math] the density of the planet. The size of the planet is immaterial; the journey time is the same if the density is the same.
In fiction
In the 2012 movie Total Recall, a gravity train called "The Fall" goes through the center of the Earth to commute between Western Europe and Australia.[5][6]
See also
- Brachistochrone curve
- Funicular
- Hyperloop
- Rail energy storage
- Schuler tuning
- Colonization of the asteroid belt
- Space elevator
References
- ↑ Newton, Isaac. Philosophiæ Naturalis Principia Mathematica. https://archive.org/details/philosophiaenatu28233gut.
- ↑ "To Everywhere in 42 Minutes". Time. February 11, 1966. https://content.time.com/time/subscriber/article/0,33009,842469-1,00.html.
- ↑ Robin Davis: A Physicist's Pipe Dream[yes|permanent dead link|dead link}}]
- ↑ Klotz, Alexander R. (2015). "The gravity tunnel in a non-uniform Earth". American Journal of Physics 83 (3): 231–237. doi:10.1119/1.4898780. Bibcode: 2015AmJPh..83..231K.
- ↑ Martinez, Jason (2012-08-13). "The Science of Total Recall". Wolfram-Alpha Blog. http://blog.wolframalpha.com/2012/08/13/the-science-of-total-recall/. Retrieved March 30, 2018.
- ↑ Rothman, Lily (August 6, 2012). "Spoiler Alert: The 8,000-Mile Hole in Total Recall". Time (magazine). http://entertainment.time.com/2012/08/06/spoiler-alert-the-8000-mile-hole-in-total-recall/. Retrieved March 30, 2018.
- Description of the concept Gravity train and mathematical solution (Alexandre Eremenko web page at Purdue University).
External links
- A simulation of this motion; includes tunnels that do not pass through the center of the earth. Also shows a satellite with same period.
- The Gravity Express
- To Everywhere in 42 Minutes
 |  |
